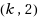The shortest-path problem with resource constraints with (k,2)-loop elimination and its application to the capacitated arc-routing problem

In many branch‐and‐price algorithms, the column generation subproblem consists of computing feasible constrained paths. In the capacitated arc‐routing problem (CARP), elementarity constraints concerning the edges to be serviced and additional constraints resulting from the branch‐and‐bound process together impose two types of loop‐elimination constraints. To fulfill the former constraints, it is common practice to rely on a relaxation where loops are allowed. In a k‐loop elimination approach all loops of length k and smaller are forbidden. Following Bode and Irnich (2012) for solving the CARP, branching on followers and non‐followers is the only known approach to guarantee integer solutions within branch‐and‐price. However, it comes at the cost of additional task‐2‐loop elimination constraints. In this paper, we show that a combined $(k\text{,}2)$ ‐loop elimination in the shortest‐path subproblem can be accomplished in a computationally efficient way. Overall, the improved branch‐and‐price often allows the computation of tighter lower bounds and integer optimal solutions for several instances from standard benchmark sets.