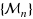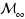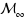| Article ID: | iaor20142002 |
| Volume: | 238 |
| Issue: | 2 |
| Start Page Number: | 486 |
| End Page Number: | 496 |
| Publication Date: | Oct 2014 |
| Journal: | European Journal of Operational Research |
| Authors: | Guo Xianping, Zhang Wenzhao |
| Keywords: | decision |
In this paper we consider the convergence of a sequence