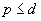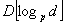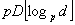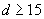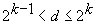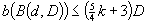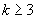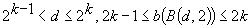The authors prove that, for any 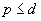 , there exists a spanning directed p-ary tree of depth at most
, there exists a spanning directed p-ary tree of depth at most 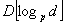 in a de Bruijn digraph B(d, D) or in a Kautz digraph K(d, D) of degree d and diameter D. This result gives directly an upper bound of
in a de Bruijn digraph B(d, D) or in a Kautz digraph K(d, D) of degree d and diameter D. This result gives directly an upper bound of 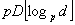 on the broadcast time of these digraphs, which improves the previously known bounds for
on the broadcast time of these digraphs, which improves the previously known bounds for 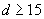 . In the case of de Bruijn digraphs, an upper bound on the broadcast time of B(pq, D) in terms of the broadcast times of B(p, D) and B(q, D) is established. This is used to improve the upper bounds on the broadcast time of B(d, D). The authors obtain several results which are refinements of the following general statements: (i) for any
. In the case of de Bruijn digraphs, an upper bound on the broadcast time of B(pq, D) in terms of the broadcast times of B(p, D) and B(q, D) is established. This is used to improve the upper bounds on the broadcast time of B(d, D). The authors obtain several results which are refinements of the following general statements: (i) for any  ,
,  , if
, if 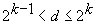 ,
, 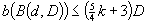 , (ii) for any
, (ii) for any 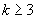 , if
, if 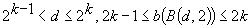 .
.