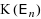| Article ID: | iaor20127400 |
| Volume: | 113 |
| Issue: | 1-2 |
| Start Page Number: | 34 |
| End Page Number: | 38 |
| Publication Date: | Jan 2013 |
| Journal: | Information Processing Letters |
| Authors: | Zawidzki Micha, Schmidt Renate A, Tishkovsky Dmitry |
| Keywords: | NP-complete |
This paper provides a proof of