The travelling salesman problem (TSP) is one of the most prominent NP‐hard combinatorial optimisation problems. After over fifty years of intense study, the TSP continues to be of broad theoretical and practical interest. Using a novel approach to empirical scaling analysis, which in principle is applicable to solvers for many other problems, we demonstrate that some of the most widely studied types of TSP instances tend to be much easier than expected from previous theoretical and empirical results. In particular, we show that the empirical median run‐time required for finding optimal solutions to so‐called random uniform Euclidean (RUE) instances – one of the most widely studied classes of TSP instances – scales substantially better than
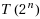with the number n of cities to be visited. The Concorde solver, for which we achieved this result, is the best‐performing exact TSP solver we are aware of, and has been applied to a broad range of real‐world problems. Furthermore, we show that even when applied to a broad range of instances from the prominent TSPLIB benchmark collection for the TSP, Concorde exhibits run‐times that are surprisingly consistent with our empirical model of Concorde’s scaling behaviour on RUE instances. This result suggests that the behaviour observed for the simple random structure underlying RUE is very similar to that obtained on the structured instances arising in various applications.
