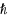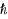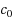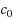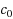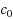Determination of optimal convergence‐control parameter value in homotopy analysis method

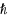In the framework of the Homotopy Analysis Method (HAM) the so‐called convergence‐control parameter $c_0$ (Liao (Int J Non‐Linear Mech 32:815–822, 1997) originally used the symbol $\hslash$ to denote the auxiliary parameter. But, 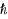$\hslash$ is well‐known as Planck’s constant in quantum mechanics. To avoid misunderstanding, Liao (Commun Nonlinear Sci Numer Simulat 15:2003–2016, 2010) suggest to use the symbol 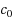$c_0$ to denote the basic convergence‐control parameter.) has a key role in convergence of obtained series solution of solving non‐linear equations. In this paper a modified approach in the determining of the convergence‐control parameter value 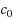$c_0$ is proposed. The purpose of this paper is to find a proper convergence‐control parameter 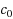$c_0$ to get a convergent series solution, or a faster convergent one. 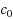This modified approach minimizes the norm of a discrete residual function, systematically, in which seeks to find an optimal value of the convergence‐control parameter $c_0$ at each order of HAM approximation, instead of the so‐called $c_0$ ‐curve process. The proved theorems and numerical results demonstrate the validity, efficiency, and performance of the proposed approach.