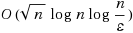Complexity analysis and numerical implementation of primal‐dual interior‐point methods for convex quadratic optimization based on a finite barrier

In this paper, we present primal‐dual interior‐point methods for convex quadratic optimization based on a finite barrier, which has been investigated earlier for the case of linear optimization by Bai et al. (2003). By means of the feature of the finite kernel function, we study the complexity analysis of primal‐dual interior‐point methods based on the finite barrier and derive the iteration bounds that match the currently best known iteration bounds for large‐ and small‐update methods, namely, $O(\sqrt{n}\log n\log \frac{n}{\epsilon })$ and $O(\sqrt{n}\log \frac{n}{\epsilon })$ , respectively, which are as good as the linear optimization analogue. Numerical tests demonstrate the behavior of the algorithms with different parameters.