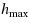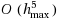Splitting extrapolation algorithms for solving the boundary integral equations of anisotropic Darcy’s equation on polygons by mechanical quadrature methods

In this paper we study the stability and convergence of the solution for the first kind integral equations of the anisotropic Darcy’s equations by the mechanical quadrature methods on closed polygonal boundaries in ℝ². Using the collectively compact theory, we construct numerical solutions which converge with the order $O(h_{\text{max}}^3)$ , where $h_{\text{max}}$ is the mesh size. In addition, An a posteriori asymptotic error representation is derived by splitting extrapolation methods in order to construct self‐adaptive algorithms, and the convergence rate $O(h_{\text{max}}^5)$ can be achieved after using the splitting extrapolation methods once. Finally, the numerical examples show the efficiency of our methods.