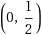Convergence analysis of high‐order compact alternating direction implicit schemes for the two‐dimensional time fractional diffusion equation

High‐order compact finite difference method with operator‐splitting technique for solving the two dimensional time fractional diffusion equation is considered in this paper. The Caputo derivative is evaluated by the L1 approximation, and the second order derivatives with respect to the space variables are approximated by the compact finite differences to obtain fully discrete implicit schemes. Alternating Direction Implicit (ADI) method is used to split the original problem into two separate one dimensional problems. One scheme is given by replacing the unknowns by the values on the previous level directly and a correction term is added for another scheme. Theoretical analysis for the first scheme is discussed. The local truncation error is analyzed and the stability is proved by the Fourier method. Using the energy method, the convergence of the compact finite difference scheme is proved. Numerical results are provided to verify the accuracy and efficiency of the two proposed algorithms. For the order of the temporal derivative lies in different intervals 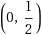$(0,\frac{1}{2})$ or $[\frac{1}{2},1)$ , corresponding appropriate scheme is suggested.