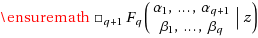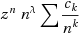Acceleration of generalized hypergeometric functions through precise remainder asymptotics

We express the asymptotics of the remainders of the partial sums {s n } of the generalized hypergeometric function 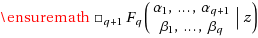$\text{syntax error at token }}$ through an inverse power series 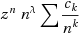$z^n{n}^{\lambda }\sum \frac{c_k}{n^k}$ , where the exponent λ and the asymptotic coefficients {c k } may be recursively computed to any desired order from the hypergeometric parameters and argument. From this we derive a new series acceleration technique that can be applied to any such function, even with complex parameters and at the branch point z = 1. For moderate parameters (up to approximately ten) a C implementation at fixed precision is very effective at computing these functions; for larger parameters an implementation in higher than machine precision would be needed. Even for larger parameters, however, our C implementation is able to correctly determine whether or not it has converged; and when it converges, its estimate of its error is accurate.