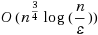| Article ID: | iaor20127274 |
| Volume: | 61 |
| Issue: | 4 |
| Start Page Number: | 659 |
| End Page Number: | 680 |
| Publication Date: | Dec 2012 |
| Journal: | Numerical Algorithms |
| Authors: | Kheirfam Behrouz |
| Keywords: | barrier function, interior point methods, primal-dual algorithm, programming (semidefinite) |
In this paper we propose primal‐dual interior‐point algorithms for semidefinite optimization problems based on a new kernel function with a trigonometric barrier term. We show that the iteration bounds are