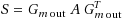Banded target matrices and recursive FSAI for parallel preconditioning

In this paper we propose a parallel preconditioner for the CG solver based on successive applications of the FSAI preconditioner. We first compute an FSAI factor G out for coefficient matrix A, and then another FSAI preconditioner is computed for either the preconditioned matrix 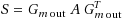$S=G_{m\mathrm{out}}A{G}_{m\mathrm{out}}^T$ or a sparse approximation of S. This process can be iterated to obtain a sequence of triangular factors whose product forms the final preconditioner. Numerical results onto large SPD matrices arising from geomechanical models account for the efficiency of the proposed preconditioner which provides a reduction of the iteration number and of the CPU time of the iterative phase with respect to the original FSAI preconditioner. The proposed preconditioner reveals particularly efficient for accelerating an iterative procedure to find the smallest eigenvalues of SPD matrices, where the increased setup cost of the RFSAI preconditioner does not affect the overall performance, being a small percentage of the total CPU time.