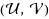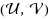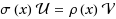In this paper, we introduce the concept of (1, 1)‐q‐coherent pair of linear functionals
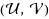 as the q‐analogue to the generalized coherent pair studied by Delgado and Marcellán (2004). This means that their corresponding sequences of monic orthogonal polynomials {P
n
(x)}
n ≥ 0 and {R
n
(x)}
n ≥ 0 satisfy
as the q‐analogue to the generalized coherent pair studied by Delgado and Marcellán (2004). This means that their corresponding sequences of monic orthogonal polynomials {P
n
(x)}
n ≥ 0 and {R
n
(x)}
n ≥ 0 satisfy
 , 0 < q < 1. We prove that if a pair of regular linear functionals
, 0 < q < 1. We prove that if a pair of regular linear functionals
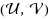 is a (1, 1)‐q‐coherent pair, then at least one of them must be q‐semiclassical of class at most 1, and these functionals are related by an expression
is a (1, 1)‐q‐coherent pair, then at least one of them must be q‐semiclassical of class at most 1, and these functionals are related by an expression
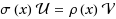 where σ(x) and ρ(x) are polynomials of degrees ≤ 3 and 1, respectively. Finally, the q‐classical case is studied.
where σ(x) and ρ(x) are polynomials of degrees ≤ 3 and 1, respectively. Finally, the q‐classical case is studied.