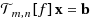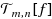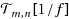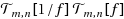BTTB preconditioners for BTTB systems

In this paper, we consider solving the BTTB system 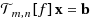${\mathcal{T}}_{m,n}[f]\mathbf{x}=\mathbf{b}$ by the preconditioned conjugate gradient (PCG) method, where 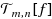${\mathcal{T}}_{m,n}[f]$ denotes the m × m block Toeplitz matrix with n × n Toeplitz blocks (BTTB) generated by a (2π, 2π)‐periodic continuous function f(x, y). We propose using the BTTB matrix 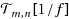${\mathcal{T}}_{m,n}[1/f]$ to precondition the BTTB system and prove that only O(m) + O(n) eigenvalues of the preconditioned matrix 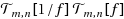${\mathcal{T}}_{m,n}[1/f]{\mathcal{T}}_{m,n}[f]$ are not around 1 under the condition that f(x, y) > 0. We then approximate 1/f(x, y) by a bivariate trigonometric polynomial, which can be obtained in O(m n log(m n)) operations by using the fast Fourier transform technique. Numerical results show that our BTTB preconditioner is more efficient than block circulant preconditioners.