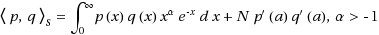| Article ID: | iaor20123758 |
| Volume: | 60 |
| Issue: | 1 |
| Start Page Number: | 51 |
| End Page Number: | 73 |
| Publication Date: | May 2012 |
| Journal: | Numerical Algorithms |
| Authors: | Dueas Herbert, Huertas Edmundo, Marcelln Francisco |
| Keywords: | algebra |
In this contribution we consider the asymptotic behavior of sequences of monic polynomials orthogonal with respect to a Sobolev‐type inner product