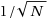Quasi‐Monte Carlo integration rules, which are equal‐weight sample averages of function values, have been popular for approximating multivariate integrals due to their superior convergence rate of order close to 1/N or better, compared to the order
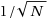of simple Monte Carlo algorithms. For practical applications, it is desirable to be able to increase the total number of sampling points N one or several at a time until a desired accuracy is met, while keeping all existing evaluations. We show that although a convergence rate of order close to 1/N can be achieved for all values of N (e.g., by using a good lattice sequence), it is impossible to get better than order 1/N convergence for all values of N by adding equally‐weighted sampling points in this manner. We then prove that a convergence of order N
− α
for α > 1 can be achieved by weighting the sampling points, that is, by using a weighted compound integration rule. We apply our theory to lattice sequences and present some numerical results. The same theory also applies to digital sequences.
