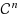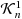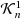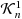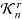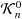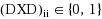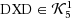| Article ID: | iaor2014278 |
| Volume: | 7 |
| Issue: | 8 |
| Start Page Number: | 1669 |
| End Page Number: | 1679 |
| Publication Date: | Dec 2013 |
| Journal: | Optimization Letters |
| Authors: | Dr Mirjam, Dickinson Peter, Gijben Luuk, Hildebrand Roland |
| Keywords: | multidimensional scaling |
We investigate the relation between the cone