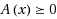An Exact Duality Theory for Semidefinite Programming Based on Sums of Squares

Farkas' lemma is a fundamental result from linear programming providing linear certificates for infeasibility of systems of linear inequalities. In semidefinite programming, such linear certificates only exist for strongly infeasible linear matrix inequalities. We provide nonlinear algebraic certificates for all infeasible linear matrix inequalities in the spirit of real algebraic geometry: A linear matrix inequality $A(x)⪰0$ is infeasible if and only if −1 lies in the quadratic module associated to A. We also present a new exact duality theory for semidefinite programming, motivated by the real radical and sums of squares certificates from real algebraic geometry.