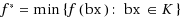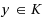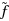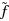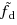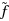| Article ID: | iaor20135222 |
| Volume: | 38 |
| Issue: | 3 |
| Start Page Number: | 418 |
| End Page Number: | 436 |
| Publication Date: | Aug 2013 |
| Journal: | Mathematics of Operations Research |
| Authors: | Lasserre Jean B |
| Keywords: | polynomial programs |
We consider the inverse optimization problem associated with the polynomial program