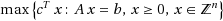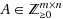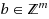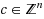The Cunningham‐Geelen Method in Practice: Branch‐Decompositions and Integer Programming

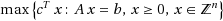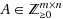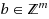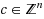In 2007, W. H. Cunningham and J. Geelen describe an algorithm for solving $\max \{c^{T}x:Ax=b,x\ge 0,x\in {\mathbb{Z}}^n\}$ , where $A\in {\mathbb{Z}}_{\ge 0}^{m\times n}$ , $b\in {\mathbb{Z}}^m$ , and $c\in {\mathbb{Z}}^n$ , which utilizes a branch‐decomposition of the matrix A and techniques from dynamic programming. In this paper, we report on the first implementation of the CG algorithm and compare our results with the commercial integer programming software Gurobi. Using branch‐decomposition trees produced by heuristics and optimal trees produced by algorithms developed in our previous studies, we test both a memory‐intensive and low‐memory version of the CG algorithm on problem instances such as graph 3‐coloring, set partition, market split, and knapsack. We isolate a class of set partition instances where the CG algorithm runs twice as fast as Gurobi, and demonstrate that certain infeasible market split and knapsack instances with width ≤6 range from running twice as fast as Gurobi, to running in a matter of minutes versus a matter of hours.