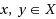On Olaleru’s open problem on Gregus fixed point theorem

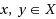Let (X, d) be a complete metric space and $\mathrm{TX}⟶X$ be a mapping with the property d(Tx, Ty) ≤ ad(x, y) + bd(x, Tx) + cd(y, Ty) + ed(y, Tx) + fd(x, Ty) for all $x,y\in X$ , where 0 < a < 1, b, c, e, f ≥ 0, a + b + c + e + f = 1 and b + c > 0. We show that if e + f > 0 then T has a unique fixed point and also if e + f ≥ 0 and X is a closed convex subset of a complete metrizable topological vector space (Y, d), then T has a unique fixed point. These results extend the corresponding results which recently obtained in this field. Finally by using our main results we give an answer to the Olaleru’s open problem.