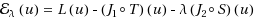| Article ID: | iaor20134037 |
| Volume: | 56 |
| Issue: | 2 |
| Start Page Number: | 399 |
| End Page Number: | 416 |
| Publication Date: | Jun 2013 |
| Journal: | Journal of Global Optimization |
| Authors: | Costea Nicuor, Varga Csaba |
| Keywords: | Laplace transforms, Banach space |
In this paper we deal with a class of non‐differentiable functionals defined on a real reflexive Banach space