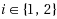A polynomial time approximation algorithm for the two‐commodity splittable flow problem

We consider a generalization of the unsplittable maximum two‐commodity flow problem on undirected graphs where each commodity 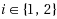$i\in \{1,2\}$ can be split into a bounded number k i of equally‐sized chunks that can be routed on different paths. We show that in contrast to the single‐commodity case this problem is NP‐hard, and hard to approximate to within a factor of α > 1/2. We present a polynomial time 1/2‐approximation algorithm for the case of uniform chunk size over both commodities and show that for even k i and a mild cut condition it can be modified to yield an exact method. The uniform case can be used to derive a 1/4‐approximation for the maximum concurrent (k 1, k 2)‐splittable flow without chunk size restrictions for fixed demand ratios.