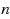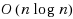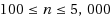Measures of problem uncertainty for scheduling with interval processing times

The paper deals with scheduling under uncertainty of the job processing times. The actual value of the processing time of a job becomes known only when the schedule is executed and may be equal to any value from the given interval. We propose an approach which consists of calculating measures of problem uncertainty to choose an appropriate method for solving an uncertain scheduling problem. These measures are based on the concept of a minimal dominant set containing at least one optimal schedule for each realization of the job processing times. For minimizing the sum of weighted completion times of the $n$ jobs to be processed on a single machine, it is shown that a minimal dominant set may be uniquely determined. We demonstrate how to use an uncertainty measure for selecting a method for finding an effective heuristic solution of the uncertain scheduling problem. The efficiency of the heuristic $O(n\log n)$ ‐algorithms is demonstrated on a set of randomly generated instances with $100\le n\le 5,000$ . A similar uncertainty measure may be applied to many other scheduling problems with interval processing times.