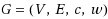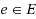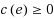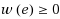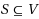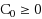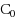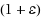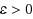| Article ID: | iaor2014188 |
| Volume: | 27 |
| Issue: | 1 |
| Start Page Number: | 32 |
| End Page Number: | 48 |
| Publication Date: | Jan 2014 |
| Journal: | Journal of Combinatorial Optimization |
| Authors: | Xue Guoliang, Ding Wei |
| Keywords: | combinatorial optimization |
Given an edge‐weighted undirected graph