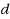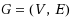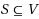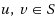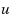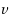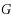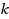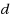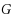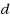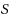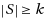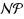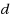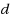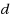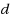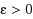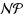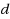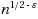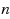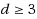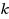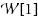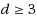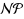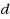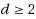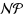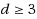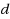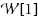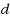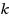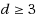The paper studies a generalization of the Independent Set problem (IS for short). A distance‐
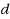 independent set for an integer
independent set for an integer
 in an unweighted graph
in an unweighted graph
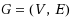 is a subset
is a subset
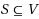 of vertices such that for any pair of vertices
of vertices such that for any pair of vertices
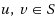 , the distance between
, the distance between
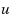 and
and
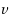 is at least
is at least
 in
in
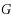 . Given an unweighted graph
. Given an unweighted graph
 and a positive integer
and a positive integer
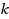 , the Distance‐
, the Distance‐
 Independent Set problem (D
Independent Set problem (D
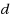 IS for short) is to decide whether
IS for short) is to decide whether
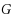 contains a distance‐
contains a distance‐
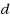 independent set
independent set
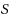 such that
such that
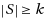 . D2IS is identical to the original IS. Thus D2IS is
. D2IS is identical to the original IS. Thus D2IS is
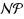 ‐complete even for planar graphs, but it is in
‐complete even for planar graphs, but it is in
 for bipartite graphs and chordal graphs. In this paper we investigate the computational complexity of D
for bipartite graphs and chordal graphs. In this paper we investigate the computational complexity of D
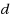 IS, its maximization version MaxD
IS, its maximization version MaxD
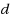 IS, and its parameterized version ParaD
IS, and its parameterized version ParaD
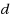 IS(
IS(
 ), where the parameter is the size of the distance‐
), where the parameter is the size of the distance‐
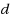 independent set: (1) We first prove that for any
independent set: (1) We first prove that for any
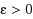 and any fixed integer
and any fixed integer
 , it is
, it is
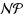 ‐hard to approximate MaxD
‐hard to approximate MaxD
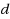 IS to within a factor of
IS to within a factor of
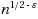 for bipartite graphs of
for bipartite graphs of
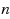 vertices, and for any fixed integer
vertices, and for any fixed integer
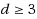 , ParaD
, ParaD
 IS(
IS(
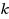 ) is
) is
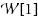 ‐hard for bipartite graphs. Then, (2) we prove that for every fixed integer
‐hard for bipartite graphs. Then, (2) we prove that for every fixed integer
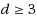 , D
, D
 IS remains
IS remains
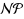 ‐complete even for planar bipartite graphs of maximum degree three. Furthermore, (3) we show that if the input graph is restricted to chordal graphs, then D
‐complete even for planar bipartite graphs of maximum degree three. Furthermore, (3) we show that if the input graph is restricted to chordal graphs, then D
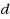 IS can be solved in polynomial time for any even
IS can be solved in polynomial time for any even
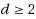 , whereas D
, whereas D
 IS is
IS is
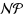 ‐complete for any odd
‐complete for any odd
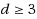 . Also, we show the hardness of approximation of MaxD
. Also, we show the hardness of approximation of MaxD
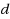 IS and the
IS and the
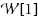 ‐hardness of ParaD
‐hardness of ParaD
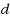 IS(
IS(
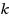 ) on chordal graphs for any odd
) on chordal graphs for any odd
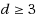 .
.