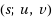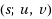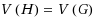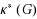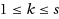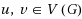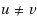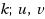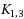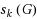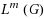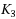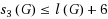Spanning 3‐connected index of graphs

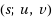For an integer $s>0$ and for $u,v\in V(G)$ with $u\ne v$ , an $(s;u,v)$ ‐path‐system of G is a subgraph H of G consisting of s internally disjoint (u, v)‐paths, and such an H is called a spanning 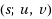$(s;u,v)$ ‐path system if 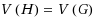$V(H)=V(G)$ . 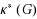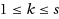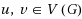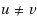The spanning connectivity ${\kappa }^{*}(G)$ of graph G is the largest integer s such that for any integer k with $1\le k\le s$ and for any $u,v\in V(G)$ with $u\ne v$ , G has a spanning ( 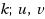$k;u,v$ )‐path‐system. Let G be a simple connected graph that is not a path, a cycle or a 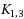$K_{\mathrm{1,3}}$ . The spanning k‐connected index of G, written 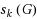$s_k(G)$ , is the smallest nonnegative integer m such that 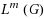$L^m(G)$ is spanning k‐connected. 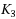Let $l(G)=\max \{m:G$ has a divalent path of length m that is not both of length 2 and in a $K_3$ }, where a divalent path in G is a path whose interval vertices have degree two in G. In this paper, we prove that 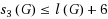$s_3(G)\le l(G)+6$ . The key proof to this result is that every connected 3‐triangular graph is 2‐collapsible.