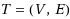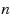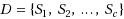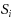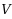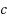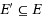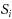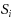Given a tree
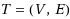 with
with
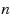 vertices and a collection of terminal sets
vertices and a collection of terminal sets
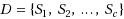 , where each
, where each
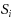 is a subset of
is a subset of
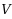 and
and
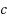 is a constant, the generalized multiway cut in trees problem (GMWC(T)) asks to find a minimum size edge subset
is a constant, the generalized multiway cut in trees problem (GMWC(T)) asks to find a minimum size edge subset
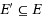 such that its removal from the tree separates all terminals in
such that its removal from the tree separates all terminals in
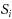 from each other for each terminal set
from each other for each terminal set
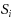 . The GMWC(T) problem is a natural generalization of the classical multiway cut in trees problem, and has an implicit relation to the Densest
‐Subgraph problem. In this paper, we show that the GMWC(T) problem is fixed‐parameter tractable by giving an
time algorithm, where
is the size of an optimal solution, and the GMWC(T) problem is polynomial time solvable when the problem is restricted in paths.We also discuss some heuristics for the GMWC(T) problem
. The GMWC(T) problem is a natural generalization of the classical multiway cut in trees problem, and has an implicit relation to the Densest
‐Subgraph problem. In this paper, we show that the GMWC(T) problem is fixed‐parameter tractable by giving an
time algorithm, where
is the size of an optimal solution, and the GMWC(T) problem is polynomial time solvable when the problem is restricted in paths.We also discuss some heuristics for the GMWC(T) problem