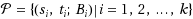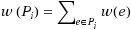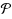We are given a digraph D=(V,A;w), a length (delay) function w:A→R
+, a positive integer d and a set
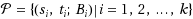 of k requests, where s
i
∈V is called as the ith source node, t
i
∈V is called the ith sink node and B
i
is called as the ith length constraint. For a given positive integer d, the subdivision‐constrained routing requests problem (SCRR, for short) is to find a directed subgraph D′=(V′,A′) of D, satisfying the two constraints: (1) Each request (s
i
,t
i
;B
i
) has a path P
i
from s
i
to t
i
in D′ with length
of k requests, where s
i
∈V is called as the ith source node, t
i
∈V is called the ith sink node and B
i
is called as the ith length constraint. For a given positive integer d, the subdivision‐constrained routing requests problem (SCRR, for short) is to find a directed subgraph D′=(V′,A′) of D, satisfying the two constraints: (1) Each request (s
i
,t
i
;B
i
) has a path P
i
from s
i
to t
i
in D′ with length
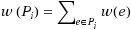 no more than B
i
; (2) Insert some nodes uniformly on each arc e∈A′ to ensure that each new arc has length no more than d. The objective is to minimize the total number of the nodes inserted on the arcs in A′. We obtain the following three main results: (1) The SCRR problem is at least as hard as the set cover problem even if each request has the same source s, i.e., s
i
=s for each i=1,2,…,k; (2) For each request (s,t;B), we design a dynamic programming algorithm to find a path from s to t with length no more than B such that the number of the nodes inserted on such a path is minimized, and as a corollary, we present a k‐approximation algorithm to solve the SCRR problem for any k requests; (3) We finally present an optimal algorithm for the case where
no more than B
i
; (2) Insert some nodes uniformly on each arc e∈A′ to ensure that each new arc has length no more than d. The objective is to minimize the total number of the nodes inserted on the arcs in A′. We obtain the following three main results: (1) The SCRR problem is at least as hard as the set cover problem even if each request has the same source s, i.e., s
i
=s for each i=1,2,…,k; (2) For each request (s,t;B), we design a dynamic programming algorithm to find a path from s to t with length no more than B such that the number of the nodes inserted on such a path is minimized, and as a corollary, we present a k‐approximation algorithm to solve the SCRR problem for any k requests; (3) We finally present an optimal algorithm for the case where
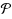 contains all possible requests (s
i
,t
i
) in V×V and B
i
is equal to the length of the shortest path in D from s
i
to t
i
. To the best of our knowledge, this is the first time that the dynamic programming algorithm within polynomial time in (2) is designed for a weighted optimization problem while previous optimal algorithms run in pseudo‐polynomial time.
contains all possible requests (s
i
,t
i
) in V×V and B
i
is equal to the length of the shortest path in D from s
i
to t
i
. To the best of our knowledge, this is the first time that the dynamic programming algorithm within polynomial time in (2) is designed for a weighted optimization problem while previous optimal algorithms run in pseudo‐polynomial time.