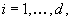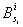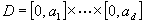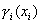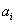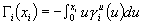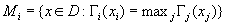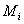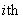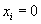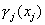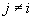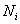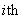For 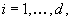 let
let 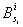 be a one-dimensional Brownian motion on the interval
be a one-dimensional Brownian motion on the interval  with absorption at the endpoints. At each instant in time, one must decide to run some subset of these d Brownian motions while holding the others fixed at their current state. The resulting process evolves in the rectangle
with absorption at the endpoints. At each instant in time, one must decide to run some subset of these d Brownian motions while holding the others fixed at their current state. The resulting process evolves in the rectangle 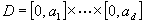 . If, at some instant, one decides to freeze all of the Brownian motions, then a reward is received in accordance with this final position. Two types of reward functions are considered. First, it is assumed that the reward is zero everywhere in D, except along the d edges that correspond to the coordinate axes. Along these edges, it is given by
. If, at some instant, one decides to freeze all of the Brownian motions, then a reward is received in accordance with this final position. Two types of reward functions are considered. First, it is assumed that the reward is zero everywhere in D, except along the d edges that correspond to the coordinate axes. Along these edges, it is given by  strictly concave functions
strictly concave functions 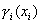 , which are zero at the endpoints 0 and
, which are zero at the endpoints 0 and 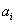 of their domains. The optimal control for this problem has a simple description. Let
of their domains. The optimal control for this problem has a simple description. Let 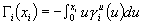 and put
and put 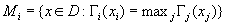 . It is proved that the optimal control is: On
. It is proved that the optimal control is: On 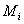 run any Brownian motion except the ith and stop the first time an edge is reached. The second class of reward functions are assumed to be zero everywhere except on the facets of D that meet at the origin. On the
run any Brownian motion except the ith and stop the first time an edge is reached. The second class of reward functions are assumed to be zero everywhere except on the facets of D that meet at the origin. On the 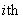 such facet (i.e., where
such facet (i.e., where 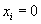 ), the reward function is the product of
), the reward function is the product of 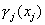 for
for 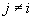 . Put
. Put  . The optimal control is: On
. The optimal control is: On 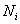 run the
run the 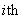 Brownian motion and stop when a facet of D is reached.
Brownian motion and stop when a facet of D is reached.