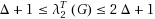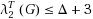L(2,1)‐labelings of the edge‐path‐replacement of a graph

For two positive integers j and k with j≥k, an L(j,k)‐labeling of a graph G is an assignment of nonnegative integers to V(G) such that the difference between labels of adjacent vertices is at least j, and the difference between labels of vertices that are distance two apart is at least k. The span of an L(j,k)‐labeling of a graph G is the difference between the maximum and minimum integers used by it. The L(j,k)‐labelings‐number of G is the minimum span over all L(j,k)‐labelings of G. This paper focuses on L(2,1)‐labelings‐number of the edge‐path‐replacement G(P k ) of a graph G. Note that G(P 3) is the incidence graph of G. L(2,1)‐labelings of the edge‐path‐replacement G(P 3) of a graph, called (2,1)‐total labeling of G, was introduced by Havet and Yu in 2002 (2008). They obtain the bound 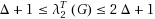$\Delta +1\le {\lambda }_2^T(G)\le 2\Delta +1$ and conjectured 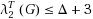${\lambda }_2^T(G)\le \Delta +3$ . In this paper, we obtain that λ(G(P k ))≤Δ+2 for k≥5, and conjecture λ(G(P 4))≤Δ+2 for any graph G with maximum degree Δ.