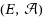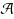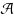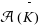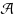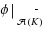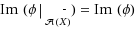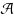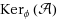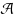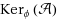Objective functions with redundant domains

Let 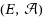$(E,𝒜)$ be a set system consisting of a finite collection 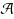$𝒜$ of subsets of a ground set E, and suppose that we have a function ϕ which maps 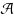$𝒜$ into some set S. Now removing a subset K from E gives a restriction 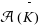$𝒜(\overline{K})$ to those sets of 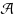$𝒜$ disjoint from K, and we have a corresponding restriction 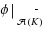$\mathrm{\varphi <!--\; ?\; -->}{|}_{\mathcal{A}(\stackrel{¯<!--\; ¯\; -->}{K})}$ of our function ϕ. If the removal of K does not affect the image set of ϕ, that is 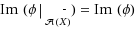$\text{Im}(\mathrm{\varphi <!--\; ?\; -->}{|}_{\mathcal{A}(\stackrel{¯<!--\; ¯\; -->}{X})})=\text{Im}(\mathrm{\varphi <!--\; ?\; -->})$ , then we will say that K is a kernel set of 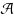$𝒜$ with respect to ϕ. Such sets are potentially useful in optimisation problems defined in terms of ϕ. We will call the set of all subsets of E that are kernel sets with respect to ϕ a kernel system and denote it by ${\mathrm{Ker}}_{\varphi }(𝒜)$ . Motivated by the optimisation theme, we ask which kernel systems are matroids. 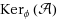For instance, if $𝒜$ is the collection of forests in a graph G with coloured edges and ϕ counts how many edges of each colour occurs in a forest then ${\mathrm{Ker}}_{\varphi }(𝒜)$ is isomorphic to the disjoint sum of the cocycle matroids of the differently coloured subgraphs; on the other hand, if 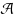$𝒜$ is the power set of a set of positive integers, and ϕ is the function which takes the values 1 and 0 on subsets according to whether they are sum‐free or not, then we show that 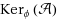${\mathrm{Ker}}_{\varphi }(𝒜)$ is essentially never a matroid.