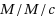This paper considers an infinite buffer
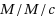queueing system in which servers follow a multi‐threshold vacation policy. With such a policy, at a service completion instant, if the number of customers in the system is less than a prefixed threshold value, part of servers together take a single vacation (or leave for a random amount of time doing other secondary job). At the vacation completion instant, they return to the system for serving the customers. Some practical production and inventory systems or call centers could be modeled as this Markovian queue with a multi‐threshold vacation policy. Using the Markovian process model, we obtain the exact closed‐form expression of rate matrix and the stationary distribution of the number of customers in the system. A cost model is developed to search the joint optimal values of the thresholds of vacation policy and service rate of each server, which minimizes the long‐term average cost. Some numerical results are presented to illustrate the optimization procedures.
