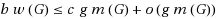For graph G, let bw(G) denote the branchwidth of G and gm(G) the largest integer g such that G contains a g×g grid as a minor. We show that bw(G)≤3 gm(G) for every planar graph G. This is an improvement over the bound bw(G)≤4 gm(G) due to Robertson, Seymour and Thomas. Our proof is constructive and implies quadratic time constant‐factor approximation algorithms for planar graphs for both problems of finding a largest grid minor and of finding an optimal branch‐decomposition: (3+ϵ)‐approximation for the former and (2+ϵ)‐approximation for the latter, where ϵ is an arbitrary positive constant. We also study the tightness of the above bound. We show that for any constant c
<2, the bound of
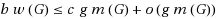does not hold in general for a planar graph G.
