From Holant to #CSP and Back: Dichotomy for Holantc Problems

We explore the intricate interdependent relationship among counting problems, considered from three frameworks for such problems: Holant Problems, counting CSP and weighted H‐colorings. We consider these problems for general complex valued functions that take boolean inputs. We show that results from one framework can be used to derive results in another, and this happens in both directions. Holographic reductions discover an underlying unity, which is only revealed when these counting problems are investigated in the complex domain ℂ. We prove three complexity dichotomy theorems, leading to a general theorem for Holant ^c problems. This is the natural class of Holant problems where one can assign constants 0 or 1. More specifically, given any signature grid on G=(V,E) over a set of symmetric functions, we completely classify the complexity to be in P or #P‐hard, according to , of 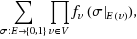$\sum _{\sigma :E\to \{\mathrm{0,1}\}}\prod _{v\in V}{f}_v(\sigma {\mid }_{E(v)}),$ where (0, 1 are the unary constant 0, 1 functions). Not only is holographic reduction the main tool, but also the final dichotomy can be only naturally stated in the language of holographic transformations. The proof goes through another dichotomy theorem on Boolean complex weighted #CSP.