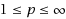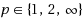The paper proposes analysis and design techniques for switching linear systems (whose commutations occur in an arbitrary manner from the internal dynamics point of view, being determined by exogenous agents). We define and characterize (by ‘if and only if’ conditions) two properties, namely (i) diagonally invariant exponential stability and (ii) diagonally invariant exponential stabilizability. Both properties rely on the existence of contractive invariant sets described by Hölder p‐norms,
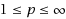, and imply the standard concepts of ‘exponential stability’ and ‘exponential stabilizability’, respectively (whereas the counter‐parts are, in general, not true). We prove that properties (i), (ii) are equivalent to a set of inequalities written for the matrix measure (associated with the p‐norm) applied to the matrices of the open‐loop system (property (i)), and, respectively, to the matrices of the closed‐loop system (property (ii)). We also develop computational instruments for testing the properties (i), (ii) in the cases of the usual p‐norms with
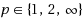. These instruments represent computable necessary and sufficient conditions for the existence of the properties (i), (ii), and whenever the property (ii) exists, a suitable state‐feedback matrix is provided. Two numerical examples are presented in order to illustrate the exploration of properties (i), (ii), as well as the use of software resources available on a powerful environment (such as MATLAB).
