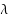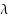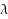Generalized equi‐statistical convergence of positive linear operators and associated approximation theorems

The concepts of equi‐statistical convergence, statistical pointwise convergence and statistical uniform convergence for sequences of functions were introduced recently by Balcerzak et al. [M. Balcerzak, K. Dems, A. Komisarski, Statistical convergence and ideal convergence for sequences of functions, J. Math. Anal. Appl. 328 (2007) 715–729]. In this paper, we use the notion of $\lambda$ ‐statistical convergence in order to generalize these concepts. We establish some inclusion relations between them. We apply our new notion of $\lambda$ ‐equi‐statistical convergence to prove a Korovkin type approximation theorem and we show that our theorem is a non‐trivial extension of some well‐known Korovkin type approximation theorems. Finally, we prove a Voronovskaja type approximation theorem via the concept of $\lambda$ ‐equi‐statistical convergence. Some interesting examples are also displayed here in support of our definitions and results.