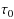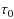Hopf bifurcation in an Internet worm propagation model with time delay in quarantine

Internet worm attacks reduce network security and cause economic losses. The use of a quarantine strategy is prominent in defending against worms, and it has been applied to various worm propagation models. Although theoretical analysis suggests that worms must get eliminated under quarantine, such a result does not appear in a real network. The time delay considered in this paper, which is caused by the time window of the intrusion detection system (IDS) that exists in the propagation system, is one of the main reasons for this. A worm propagation model with time delay under quarantine is constructed for practical application. The stability of the positive equilibrium and local Hopf bifurcation are discussed. By analysis, a critical value ${\tau }_0$ of the Hopf bifurcation is derived. When the time delay is less than ${\tau }_0$ , the worm propagation system is stable and easy to predict; when it is equal to or greater than ${\tau }_0$ , Hopf bifurcation appears. Since it is easy to control and eliminate worms under a simple and stable worm propagation system without Hopf bifurcation, the time window of the IDS must be adjusted so that the time delay is less than ${\tau }_0$ , which ensures that the worm propagation system remains stable and that worms can be eliminated with certain containment strategy. Numerical results from our experiment support our theoretical analysis.