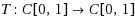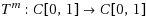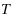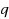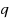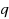| Article ID: | iaor20131396 |
| Volume: | 57 |
| Issue: | 5-6 |
| Start Page Number: | 1480 |
| End Page Number: | 1488 |
| Publication Date: | Mar 2013 |
| Journal: | Mathematical and Computer Modelling |
| Authors: | Mahmudov N I |
In this paper we prove Korovkin type theorem for iterates of general positive linear operators