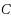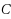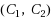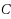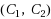| Article ID: | iaor20131341 |
| Volume: | 57 |
| Issue: | 5-6 |
| Start Page Number: | 1148 |
| End Page Number: | 1153 |
| Publication Date: | Mar 2013 |
| Journal: | Mathematical and Computer Modelling |
| Authors: | Arana M, Cambini R, Rufin A |
| Keywords: | programming: multiple criteria |
We study the minimal solutions in a nondifferentiable multiobjective problem, using a relation induced by a cone