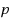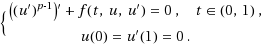| Article ID: | iaor20122217 |
| Volume: | 55 |
| Issue: | 7-8 |
| Start Page Number: | 1942 |
| End Page Number: | 1950 |
| Publication Date: | Apr 2012 |
| Journal: | Mathematical and Computer Modelling |
| Authors: | Yang Zhilin, ORegan Donal |
| Keywords: | Laplace approximation |
This paper mainly deals with the existence and multiplicity of positive solutions for the focal problem involving both the