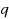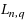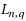| Article ID: | iaor20122210 |
| Volume: | 55 |
| Issue: | 7-8 |
| Start Page Number: | 1866 |
| End Page Number: | 1875 |
| Publication Date: | Apr 2012 |
| Journal: | Mathematical and Computer Modelling |
| Authors: | Trif Tiberiu |
| Keywords: | global convergence |
Gavrea and Trif [I. Gavrea, T. Trif, The rate of convergence by certain new Meyer‐König and Zeller operators of finite type, Rend. Circ. Mat. Palermo (2) Suppl. 76 (2005) 375–394] introduced a sequence