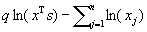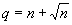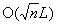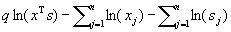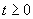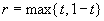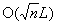Polynomial-time algorithms for linear programming based only on primal scaling and projected gradients of a potential function

This paper presents extensions and further analytical properties of algorithms for linear programming based only on primal scaling and projected gradients of a potential function. It contains extensions and analysis of two polynomial-time algorithms for linear programming. The paper first presents an extension of Gonzaga's O(nL) iteration algorithm, that computes dual variables and does not assume a known optimal objective function value. This algorithm uses only affine scaling, and is based on computing the projected gradient of the potential function where x is the vector of primal variables and s is the vector of dual slack variables, and . The algorithm takes either a primal step or recomputes dual variables at each iteration. The paper next presents an alternate form of Ye's iteration algorithm, that is an extension of the first algorithm of the paper, but uses the potential function where . This alternate form of Ye's algorithm is used to show that Ye's algorithm is optimal with respect to the choice of the parameter q in the following sense. Suppose that q=n+n^t where . Then the algorithm will solve the linear program in O(n^rL) iterations, where . Thus the value of t that minimizes the complexity bound is t=1/2, yielding Ye's iteration bound.