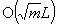Complexity analysis of a linear complementarity algorithm based on a Lyapunov function

The paper considers a path following algorithm for solving linear complementarity problems with positive semi-definite matrices. This algorithm can start from any interior solution and attain a linear rate of convergence. Moreover, if the starting solution is appropriately chosen, this algorithm achieves a complexity of iterations, where m is the number of variables and L is the size of the problem encoding in binary. The paper presents a simple complexity analysis for this algorithm, which is based on a new Lyapunov function for measuring the nearness to optimality. This Lyapunov function has itself interesting properties that can be used in a line search to accelerate convergence. The paper also develops an inexact line search procedure in which the line search stepsize is obtainable in a closed form. Finally, this algorithm was extended to handle directly variables which are unconstrained in sign and whose corresponding matrix is positive definite. The rate of convergence of this extended algorithm is shown to be independent of the number of such variables.