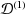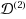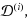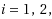Stationary distribution of a two‐dimensional SRBM: geometric views and boundary measures

We present three sets of results for the stationary distribution of a two‐dimensional semimartingale‐reflecting Brownian motion (SRBM) that lives in the non‐negative quadrant. The SRBM data can equivalently be specified by three geometric objects, an ellipse and two lines, in the two‐dimensional Euclidean space. First, we revisit the variational problem (VP) associated with the SRBM. Building on Avram et al. (2001), we show that the value of the VP at a point in the quadrant is equal to the optimal value of a linear function over a convex domain. Depending on the location of the point, the convex domain is either ${𝒟}^{(1)}$ or ${𝒟}^{(2)}$ or ${𝒟}^{(1)}\cap {𝒟}^{(2)},$ where each ${𝒟}^{(i)},$ $i=1,2,$ can easily be described by the three geometric objects. Our results provide a geometric interpretation for the value function of the VP and allow one to see geometrically when one edge of the quadrant has influence on the optimal path traveling from the origin to a destination point. Second, we provide a geometric condition that characterizes the existence of a product form stationary distribution. Third, we establish exact tail asymptotics of two boundary measures that are associated with the stationary distribution; a key step in our proof is to sharpen two asymptotic inversion lemmas in Dai and Miyazawa (2011) which allow one to infer the exact tail asymptotic of a boundary measure from the singularity of its moment‐generating function.