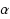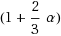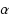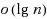Scheduling to minimize gaps and power consumption

This paper considers scheduling tasks while minimizing the power consumption of one or more processors, each of which can go to sleep at a fixed cost 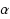$\alpha$ . There are two natural versions of this problem, both considered extensively in recent work: minimize the total power consumption (including computation time), or minimize the number of ‘gaps’ in execution. For both versions in a multiprocessor system, we develop a polynomial‐time algorithm based on sophisticated dynamic programming. In a generalization of the power‐saving problem, where each task can execute in any of a specified set of time intervals, we develop a 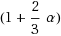$(1+\frac{2}{3}\alpha )$ ‐approximation, and show that dependence on 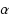$\alpha$ is necessary. In contrast, the analogous multi‐interval gap scheduling problem is set‐cover hard (and thus not 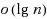$o(\lg n)$ ‐approximable), even in the special cases of just two intervals per job or just three unit intervals per job. We also prove several other hardness‐of‐approximation results. Finally, we give an 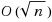$O(\sqrt{n})$ ‐approximation for maximizing throughput given a hard upper bound on the number of gaps.