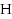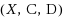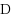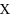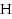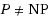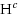Colorability of mixed hypergraphs and their chromatic inversions

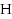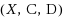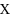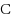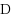We solve a long‐standing open problem concerning a discrete mathematical model, which has various applications in computer science and several other fields, including frequency assignment and many other problems on resource allocation. A mixed hypergraph ${H}$ is a triple $(X,{C},{D})$ , where ${X}$ is the set of vertices, and ${C}$ and ${D}$ are two set systems over 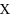${X}$ , the families of so‐called C‐edges and D‐edges, respectively. A vertex coloring of a mixed hypergraph 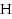${H}$ is proper if every C‐edge has two vertices with a common color and every D‐edge has two vertices with different colors. A mixed hypergraph is colorable if it has at least one proper coloring; otherwise it is uncolorable. The chromatic inversion of a mixed hypergraph ${H}=(X,{C},{D})$ is defined as ${{H}}^c=(X,{D},{C})$ . Since 1995, it was an open problem wether there is a correlation between the colorability properties of a hypergraph and its chromatic inversion. 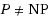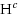In this paper we answer this question in the negative, proving that there exists no polynomial‐time algorithm (provided that $P\ne \mathrm{NP}$ ) to decide whether both ${H}$ and ${{H}}^c$ are colorable, or both are uncolorable. This theorem holds already for the restricted class of 3‐uniform mixed hypergraphs (i.e., where every edge has exactly three vertices). The proof is based on a new polynomial‐time algorithm for coloring a special subclass of 3‐uniform mixed hypergraphs. Implementation in C++ programming language has been tested. Further related decision problems are investigated, too.