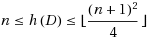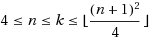| Article ID: | iaor20132807 |
| Volume: | 25 |
| Issue: | 4 |
| Start Page Number: | 694 |
| End Page Number: | 701 |
| Publication Date: | May 2013 |
| Journal: | Journal of Combinatorial Optimization |
| Authors: | Chang Ting-Pang, Tong Li-Da |
| Keywords: | combinatorial optimization |
In the paper, we study the hamiltonian numbers in digraphs. A hamiltonian walk of a digraph