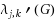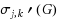Distance two edge labelings of lattices

Suppose G is a graph. Two edges e and e′ in G are said to be adjacent if they share a common end vertex, and distance two apart if they are nonadjacent but both are adjacent to a common edge. Let j and k be two positive integers. An L(j,k)‐edge‐labeling of a graph G is an assignment of nonnegative integers, called labels, to the edges of G such that the difference between labels of any two adjacent edges is at least j, and the difference between labels of any two edges that are distance two apart is at least k. The minimum range of labels over all L(j,k)‐edge‐labelings of a graph G is called the L(j,k)‐edge‐labeling number of G, denoted by 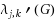${\lambda }_{j,k}\prime (G)$ . Let m, j and k be positive integers. An m‐circular‐L(j,k)‐edge‐labeling of a graph G is an assignment f from {0,1,…,m−1} to the edges of G such that, for any two edges e and e′, |f(e)−f(e′)| m ≥j if e and e′ are adjacent, and |f(e)−f(e′)| m ≥k if e and e′ are distance two apart, where |a| m =min{a,m−a}. The minimum m such that G has an m‐circular‐L(j,k)‐edge‐labeling is called the circular‐L(j,k)‐edge‐labeling number of G, denoted by 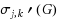${\sigma }_{j,k}\prime (G)$ . This paper investigates the L(1,1)‐edge‐labeling numbers, the L(2,1)‐edge‐labeling numbers and the circular‐L(2,1)‐edge‐labeling numbers of the hexagonal lattice, the square lattice, the triangular lattice and the strong product of two infinite paths.