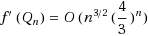A pebbling move consists of removing two pebbles from one vertex and then placing one pebble at an adjacent vertex. If a distribution δ of pebbles lets us move at least one pebble to each vertex by applying pebbling moves repeatedly(if necessary), then δ is called a pebbling of G. The optimal pebbling number
f′(G) of G is the minimum number of pebbles used in a pebbling of G. In this paper, we improve the known upper bound for the optimal pebbling number of the hypercubes Q
n
. Mainly, we prove for large n,
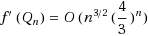by a probabilistic argument.
